Tendon Biomechanics
Original Editors - Evan Thomas
Top Contributors - Evan Thomas, Lucinda hampton, Simisola Ajeyalemi, Kim Jackson, Wanda van Niekerk, WikiSysop, Claire Knott, Rucha Gadgil, 127.0.0.1 and Admin
Tendon Structure & Composition[edit | edit source]
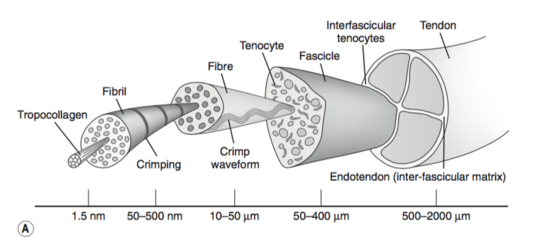
Tendons have a hierarchical arrangement that is sequentially composed of collagen molecules, fibrils, fibres, fascicles, and lastly the tendon unit. Tendon units are encased in epitenon, which reduces friction with neighbouring tissues.[1]
The tensile strength of a tendon is dependent on collagen.
- Type I collagen comprises approximately 70–80% of the dry weight of a normal tendon.
- Many other types of collagen are also present, including type III (functions to form rapid cross-links in stabilizing repair sites in torn tendons), type V (regulates collagen fibril diameter), and type XII (provides lubrication between collagen fibres).[1]
Additionally to collagen, many proteoglycans (e.g. aggrecan and decorin) and glycoproteins (e.g. elastin, fibronectin, and tenascin-C) also have important functions in tendons.
- Aggrecan binds water and resists compression
- Decorin promotes fibrillar slippage.
- Elastin, fibronectin, and tenascin-C function to enhance mechanical stability, aid tendon healing, and allow tendons to revert back to their pre-stretched lengths after normal physiological loading, respectively.[1]
For more on tendon anatomy, refer here.
Tendon Mechanical Properties: Non-Linear Elasticity[edit | edit source]
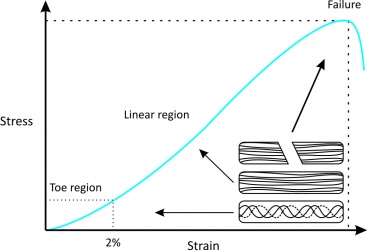
The structure and composition of tendons allow for their unique mechanical behaviour, reflected by a stress-strain curve consisting of three distinct regions (Fig. 1):[2]
|
Figure 1[2] |
Since there are many muscles in the body, each tendon differs in its function and therefore its mechanical properties.[1] For example, the Young’s modulus of the human patellar tendon is 660 ± 266 MPa (mean ± standard deviation),[3] whereas the tibialis anterior tendon is about 1200 MPa.[4] Aging also significantly affects the mechanical properties of tendons:[1] Young’s modulus of human patellar tendons aged 29–50 years is about 660 ± 266 MPa, but is about 504 ± 222 MPa in those aged 64–93 years.[3]
Tendon Mechanical Properties: Viscoelasticity[edit | edit source]
Tendons also have viscoelastic properties (likely the result of collagenous proteins, water, and the interactions between collagens and proteoglycans), meaning their mechanical behaviour is dependent on the rate of mechanical strain.[1] In other words, the relationship between stress and strain for a tendon is not constant but depends on the time of displacement or load.[2] A viscoeleastic material is more deformable at low strain rates but less deformable at high strain rates. Therefore, tendons at low strain rates tend to absorb more mechanical energy but are less effective in carrying mechanical loads. However, tendons become stiffer and more effective in transmitting large muscular loads to bone at high strain rates.[1]
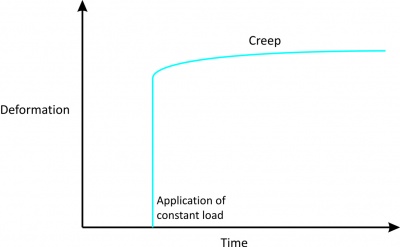
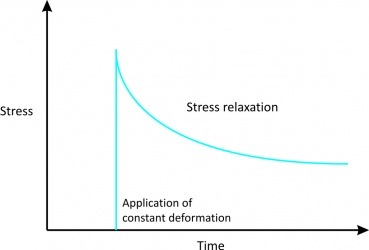
There are three major characteristics of a viscoelastic material of tendons:[2]
|
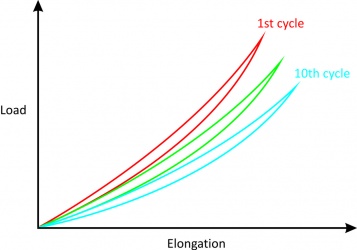
1. Creep
|
Figure 2[2] |
|
2. Stress relaxation
|
Figure 3[2] |
|
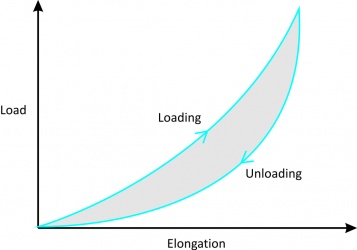
3. Hysteresis or energy dissipation
|
Figure 4[2]
Figure 5[2] |
Factors Affecting Mechanical Forces[edit | edit source]
Many factors affect the mechanical forces on tendons during normal locomotion.[5]
- First, different tendons in the body are subjected to different levels of mechanical loads.[6] For example, it has been estimated that the peak force transmitted through the Achilles tendon in humans during running is 9 kN, which is equivalent to 12.5 times body weight.[7] In human hand flexor tendons, it has been shown that the intra-tendinous force of the tendon depends on whether the force is generated passively or actively, and whether the position of the joint is in flexion or extension. During passive mobilization of the wrist, the flexor tendon force was found to be between 1-6 N and up to 9 N during similar mobilization of the fingers. During a 35 N fingertip pinch, tendon forces can be measured up to 12 N whereas during active, unresisted finger motion, tendon force can reach approximately 35 N.[8]
- Second, both the level of muscle contraction and the tendon’s relative size influence mechanical forces on a tendon. In general, the greater the cross-sectional area of a muscle, the higher force it can produce and the larger stress its tendon undergoes (e.g. patellar tendon vs. hamstring).[9]
- Third, different activities induce different levels of forces, even on the same tendon (in animal models).[10] Similarly, varying the rate and frequency of mechanical loading results in different tendon forces.[11][12]
The Differential Effects of Mechanical Loading on Tendons[1][edit | edit source]
| Mechanical Load Level | Effects on Tendon |
|---|---|
|
Low |
• ↓ Tensile strength |
|
Moderate |
• ↑ Tensile strength |
|
Excessive |
• ↓ Tensile strength |
It can be seen from the above that in general[1], mechanical loading at physiological levels is beneficial to tendons, but excessive loading or disuse of tendons is detrimental
Normal tendons can show a disorganised response to loading as well as improved tendon structure with over long term loading. Normal tendons in Australian football athletes have been shown on UTC imaging to demonstrate disorganisation as a normal response to the mechanical loading of a game, this disorganisation returned to normal after 4 days[13]. In the same research series the Australian football players showed an improvement in tendon structure over a 5 month pre season training period with increased fibrillar alignment[14].
Resources[edit | edit source]
The Physioology of Sports Injuries and Repair Processes (Chapter) by Robi K, Jakob N, Matevz K, and Matjaz V (2013)
References[edit | edit source]
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 Wang JHC, Guo Q, Li B. Tendon Biomechanics and Mechanobiology - A Minireview of Basic Concepts and Recent Advancements. Journal of Hand Therapy, 2012; 25(2):133–141.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 Robi K, Jakob N, Matevz K, Matjaz V (2013). Chapter 2: The Physiology of Sports Injuries and Repair Processes. In Hamlin M (Ed.), ISBN: 978-953-51-1031-6, InTech, DOI: 10.5772/54234.
- ↑ 3.0 3.1 Johnson GA, Tramaglini DM, Levine RE, Ohno K, Choi NY, Woo SL. Tensile and viscoelasticfckLRproperties of human patellar tendon. J Orthop Res, 1994; 12(6): 796–803.
- ↑ Maganaris CN, Paul JP. In vivo human tendon mechanical properties. J Physiol, 1999; 521 (Pt 1): 307–313.
- ↑ Wang, JHC. Mechanobiology of Tendon. Journal of Biomechanics, 2006; 39: 1563–1582.
- ↑ Maganaris CN. Tensile properties of in vivo human tendinous tissue. Journal of Biomechanics, 2002; 35: 1019–1027.
- ↑ Komi PV, Fukashiro S, Jarvinen M. Biomechanical loading of Achilles tendon during normal locomotion. Clinics in Sports Medicine, 1992; 11: 521–531.
- ↑ Schuind F, Garcia-Elias M, Cooney WP, An KN. fckLRFlexor tendon forces: in vivo measurements. Journal of Hand Surgery [American], 1992; 17: 291–298.
- ↑ Kellis E. Quantification of quadriceps and hamstring antagonist activity. Sports Medicine, 1998; 25: 37–62.
- ↑ Korvick DL, Cummings JF, Grood ES, Holden JP, Feder SM, Butler DL. The use of an implantable force transducer to measure patellar tendon forces in goats. Journal of Biomechanics, 1996; 29: 557–561.
- ↑ Finni T, Komi PV, Lukkariniemi J. Achilles tendon loading during walking: application of a novel optic fiber technique. European Journal of Applied Physiology and Occupational Physiology, 1998; 77: 289–291.
- ↑ Kyrolainen H, Finni T, Avela J, Komi PV. Neuromuscular behaviour of the triceps surae muscle-tendon complex during running and jumping. International Journal of Sports Medicine, 2003; 24: 153–155.
- ↑ Samuel D Rosengarten1, Jill L Cook, Adam L Bryant, Justin T Cordy, John Daffy, Sean I Docking. Australian football players’ Achilles tendons respond to game loads within 2 days: an ultrasound tissue characterisation (UTC) study. Br J Sports Med 2015;49:183-187
- ↑ Docking SI, Rosengarten SD, Cook J1. Achilles tendon structure improves on UTC imaging over a 5-month pre-season in elite Australian football players. Scand J Med Sci Sports. 2015 May 5.